How can we make sure autonomous vehicles don’t drive into anything in their environment? How can CNC machines or 3D printers fabricate delicate parts, or print an entire house, without colliding with the workpiece or the machinery itself?
Bounding volume hierarchies are data structures which allow efficient solving of collision detection problems and distance computation between possibly very complex objects. Collision detection asks whether or not two complex objects – or an object and a very simple geometric query object – collide or intersect one another. Distance computation (or a closest point computation) finds the point on the surface of the object which is closest to the query. This can be a vertex, or a point lying on one of the faces.
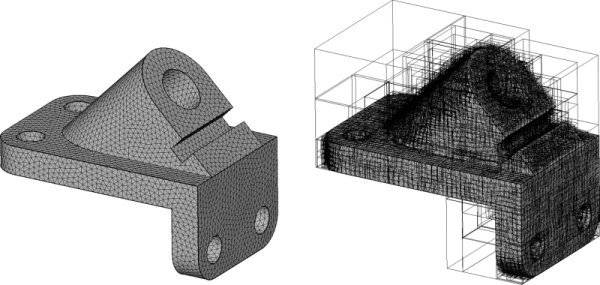
Bounding volume hierarchies approximate the objects to be queried using a hierarchy of simple bounding volumes (see image above). Each of these encloses some subset of the primitives (usually triangles) which comprise the object. To perform an intersection query between an object and a line for instance, this hierarchy is traversed. Traversal starts from the root node, which is the bounding volume which contains the entire object, and proceeds recursively to ever smaller portions of the object. This generally results in massive performance improvements over having to test all of the primitives. Unlike uniform grids and k-d trees, BVHs have accurately predictable memory requirements, and usually require less memory. In general, queries are faster than with uniform grids, but slightly slower than k-d trees. BVHs support object-object intersections.
We are upgrading the 3D Fast Intersection and Distance Computation (AABB Tree) package in the Computational Geometry Algorithms Library (CGAL), to make it applicable to a wider range of problems and to improve its performance.
Recent work has allowed the use of:
Future work involves implementing:
Interested in writing a thesis? Contact one of our project members!
| Name | Telefon | Raum | |
|---|---|---|---|
| Dr. Michael Hemmer |
Bei weiteren Fragen wenden Sie sich bitte an die Projektmitglieder.
Technische Universität Braunschweig
Universitätsplatz 2
38106 Braunschweig
Postfach: 38092 Braunschweig
Telefon: +49 (0) 531 391-0