Mit Graphen lassen sich zahllose diskrete Strukturen darstellen. Zugleich beruhen sehr viele algorithmische Probleme auf der Betrachtung von Graphen. In diesem Kapitel werden wir eines davon betrachten: Wann und wie lassen sich alle Kanten eines Graphen in einem Zug ablaufen, ohne abzusetzen?
Termine:
- Vorlesung 2 am 03.11.20 (09:45 Uhr): Graphen und Eulertouren
- Vorlesung 3 am 04.11.20 (11:30 Uhr): Wege in Graphen
- Übung 2 am 05.11.20 (11:30 Uhr): Beweistechniken (Teil 1)
- Vorlesung 4 am 10.11.20 (09:45 Uhr): Bedingungen für Eulertouren
Vorlesungen
-
Vorlesung 4
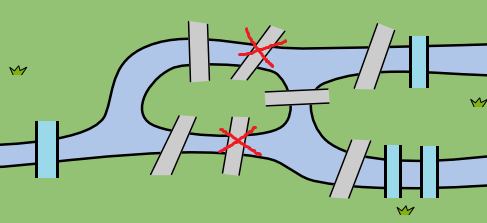In dieser Vorlesung werden notwendige Bedingungen für Eulertouren erleutert. Zusätzlich wird das Kapitel 2 noch einmal zusammengefasst. -
Übung 2
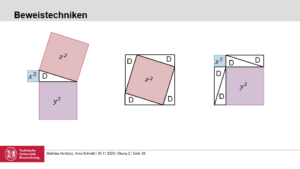In dieser Übung betrachten wir erste Methoden, um mathematische Aussagen zu beweisen. -
Vorlesung 3
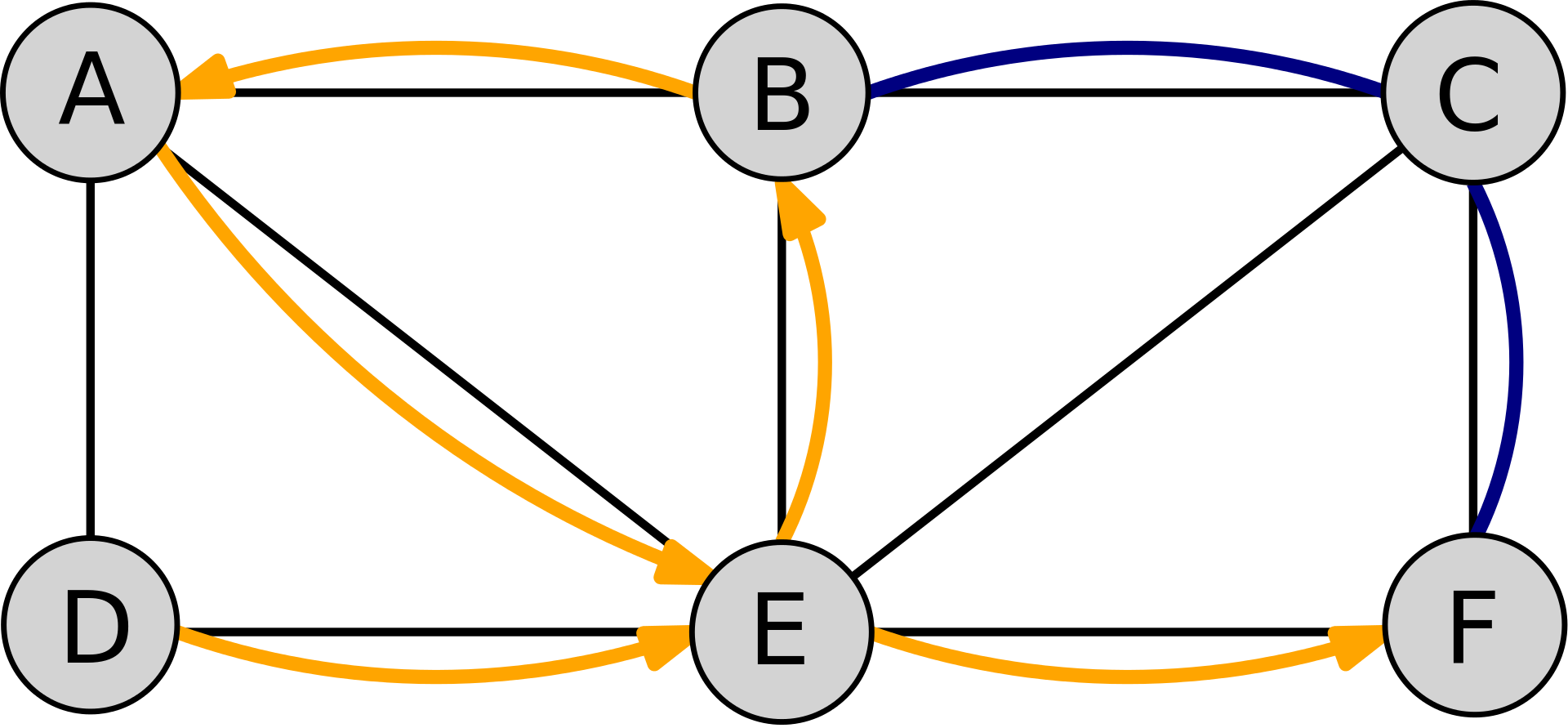In dieser Vorlesung beschäftigen wir uns mit der formalen Definition von Graphen und Wegen in Graphen. -
Vorlesung 2
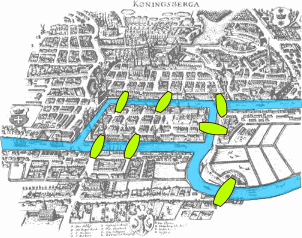In dieser Vorlesung werden Graphen eingeführt und verschiedene verwandte Probleme besprochen.